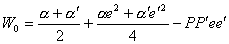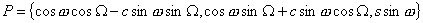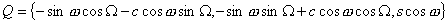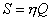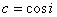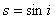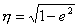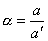Метод
Каталоги
Контакты
С разрешения профессора университета К. В. Холшевникова здесь размещается подраздел статьи "Топология и метрика пар кеплеровских орбит", опубликованный в "Физика Космоса: труды 30-й студенческой научной конференции"1 В этом подразделе предложены четыре естественных метрики. В курсовой работе была вычислена четвертая метрика (формула 18), соответствующая минимальному среднеквадратическому расстоянию между двумя кеплеровскоми орбитами как точками в пятимерном пространстве Е кеплеровских орбит.
К. В. Холшевников
Санкт-Петербургский государственный университет
Естественные метрики в пространстве кеплеровских орбит.
Будем теперь считать Е точкой в пятимерном пространстве Е кеплеровских эллипсов. Построим несколько естественных метрик ρ(Е1,Е2) в Е. Малость ρ означает, что орбиты Е1, Е2 почти совпадают.
Для построения расстояния представляется естественным сравнивать точки с одинаковой эксцентрической аномалией. Таким путем получаем равномерную и среднеквадратическую метрики
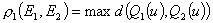 (10)
(10)
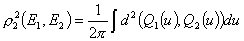 (11)
(11)
Наибольшее значение и интеграл берутся по отрезку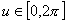 .
.
Легко доказать, что все аксиомы метрического пространства выполнены для обеих метрик (10), (11), если исключить круговые орбиты. Иными словами, расстояния (10), (11) определены и топологически эквивалентны в пространстве E0 некруговых эллиптических орбит. Они разрывны в окрестности хотя бы одной круговой орбиты из пары. Причина очевидна. Например, две компланарные орбиты с одинаковой большой полуосью и почти нулевыми эксцентриситетами почти совпадают независимо от направления апсид. Но оба расстояния существенно зависят от их направления. Чтобы избежать неприятностей, мы должны сравнивать точки, имеющие различные взаимные положения. Хороший способ — ввести следующие метрики:
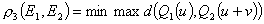 (12)
(12)
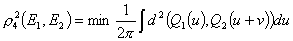 (13)
(13)
Наибольшее значение и интеграл берутся по отрезку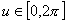 , наименьшее значение — по отрезку
, наименьшее значение — по отрезку 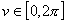 .
.
Все аксиомы метрического пространства выполнены для обеих метрик (12), (13) во всем пространстве Е, хотя доказательство много сложнее, чем в предыдущем случае, Расстояния (12), (13) топологически эквивалентны и превращают Е в открытое, неограниченное, локально-компактное метрическое пространство. Приведем алгоритмы определения расстояний ρk.
1. Обозначим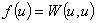 . Очевидно,
. Очевидно,
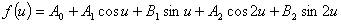 , (14)
, (14)
где
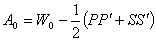 ,
,
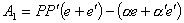 ,
,
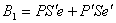 ,
,
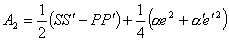 ,
, 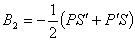 .
.
Первый шаг состоит в нахождении всех вещественных, лежащих на окружности [0,2π) корней уравнения
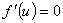 , (15)
, (15)
где
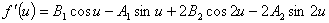 .
.
Обозначим через u0 один из корней (15), дающий наибольшее значение f.
Тогда
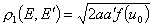 . (16)
. (16)
2. Интеграл (11) элементарен. Для второго расстояния получаем простую формулу
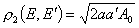 . (17)
. (17)
3. Алгоритм вычисления третьего расстояния столь сложен, что мы не рекомендуем использовать его на практике.
4. Интеграл в (13) элементарен
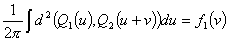
Здесь
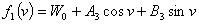 ,
,
где
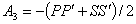 ,
, 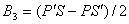 .
.
Поскольку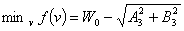 , получаем окончательно
, получаем окончательно
Для того, чтобы вычислить расстояние (метрику), понадобятся еще несколько формул: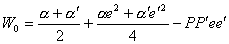
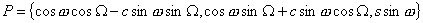
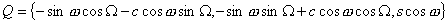
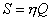
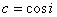
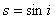
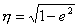
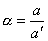
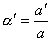
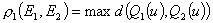 (10)
(10)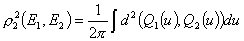 (11)
(11)Наибольшее значение и интеграл берутся по отрезку
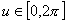 .
.Легко доказать, что все аксиомы метрического пространства выполнены для обеих метрик (10), (11), если исключить круговые орбиты. Иными словами, расстояния (10), (11) определены и топологически эквивалентны в пространстве E0 некруговых эллиптических орбит. Они разрывны в окрестности хотя бы одной круговой орбиты из пары. Причина очевидна. Например, две компланарные орбиты с одинаковой большой полуосью и почти нулевыми эксцентриситетами почти совпадают независимо от направления апсид. Но оба расстояния существенно зависят от их направления. Чтобы избежать неприятностей, мы должны сравнивать точки, имеющие различные взаимные положения. Хороший способ — ввести следующие метрики:
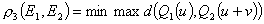 (12)
(12)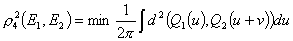 (13)
(13)Наибольшее значение и интеграл берутся по отрезку
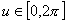 , наименьшее значение — по отрезку
, наименьшее значение — по отрезку 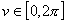 .
.Все аксиомы метрического пространства выполнены для обеих метрик (12), (13) во всем пространстве Е, хотя доказательство много сложнее, чем в предыдущем случае, Расстояния (12), (13) топологически эквивалентны и превращают Е в открытое, неограниченное, локально-компактное метрическое пространство. Приведем алгоритмы определения расстояний ρk.
1. Обозначим
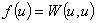 . Очевидно,
. Очевидно,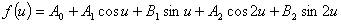 , (14)
, (14)где
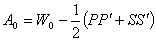 ,
, 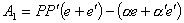 ,
,
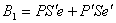 ,
, 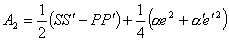 ,
, 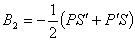 .
.Первый шаг состоит в нахождении всех вещественных, лежащих на окружности [0,2π) корней уравнения
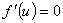 , (15)
, (15)где
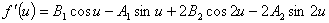 .
.Обозначим через u0 один из корней (15), дающий наибольшее значение f.
Тогда
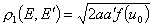 . (16)
. (16)2. Интеграл (11) элементарен. Для второго расстояния получаем простую формулу
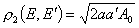 . (17)
. (17)3. Алгоритм вычисления третьего расстояния столь сложен, что мы не рекомендуем использовать его на практике.
4. Интеграл в (13) элементарен
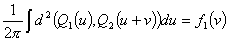
Здесь
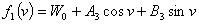 ,
,где
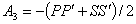 ,
, 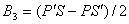 .
.Поскольку
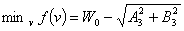 , получаем окончательно
, получаем окончательно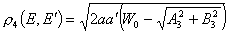 (18).
(18).
1Холшевников К. В. Естественные метрики в пространстве кеплеровских орбит // Физика Космоса: Труды 30-й Международной студенческой научной конференции, Екатеринбург, 29 января - 2 февраля 2001 г. Екатеринбург, 2001. С. 145-153.
Для того, чтобы вычислить расстояние (метрику), понадобятся еще несколько формул: